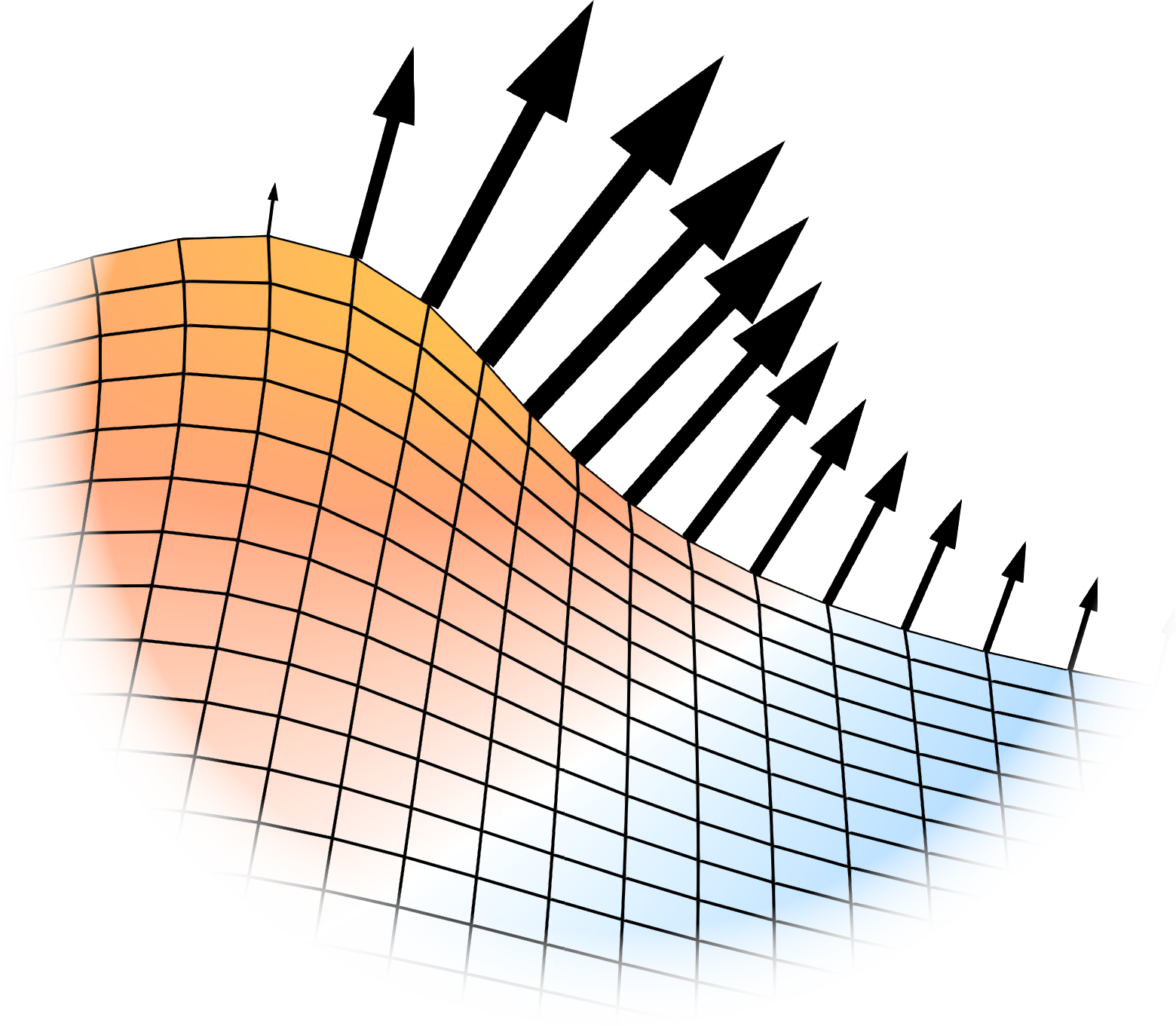
General concept for Mesh Velocity boundary conditions
Summary
All mesh velocity boundary conditions are meant to calculate the velocity of a moving boundary which should be specified for the point-vector-field pointMotionU. All boundary conditions share some common functionality which is controlled by the following settings and further explained below:
| Property | Description | Required | Default value |
|---|---|---|---|
| linearUpwindBlendingFactor | blending between linear and upwind for the face-to-point interpolation (1 corresponds to full linear and 0 corresponds to full upwind interpolation) | yes | |
| laplaceSmoothing | apply lapalace smoothing? | no | no |
Interpolation from face values to point values
All boundary conditions have in common that the value for the boundary velocity is first calculated on the patch faces and then interpolated onto the patch points. Further, only the surface-normal component of the velocity is considered as this is the only component that will have an effect on the surface topology. The interpolation from face values to point values is necessary as in order to move the mesh, the mesh points need to be moved. All quantities of interest can however only be calculated at the boundary faces in a meaningful way.
In the following, let \(V_f\) be the face-normal velocity and \(V_p\) the point-normal velocity of the surface. Due to a potential misalignment of the face normal \(\mathbf{n}_f\) and the point normal \(\mathbf{n}_p\), the surface-normal velocity is corrected when evaluated at one of its corner points. The correction is done according to \[ V_{f(p)} = \frac{V_f}{\mathbf{n}_f \cdot \mathbf{n}_p}. \]
For the interpolation, a combination of upwind and linear interpolation is used. To properly define both, consider a mesh point and all its surrounding faces. In the following all properties corresponding to the faces will be given the upper index \(^{(i)}\). It indicates the index of the corresponding face. With this, linear interpolation of the mesh velocity from the faces to the point \(V_{p, linear}\) is defined as \[ V_{p, linear} = \sum_i w^{(i)} \frac{V_f^{(i)}}{\mathbf{n}_f^{(i)} \cdot \mathbf{n}_p}. \]
\(w^{(i)}\) is an interpolation weight which is based on the inverse distance between the mesh point and the midpoint of face \(i\).
Upwind interpolation of the mesh velocity from the faces to the point \(V_{p, upwind}\) is defined as \[ V_{p, upwind} = \frac{V_f^{(j)}}{\mathbf{n}_f^{(j)} \cdot \mathbf{n}_p}, \] with \[ j = \operatorname*{argmax}_i \frac{\mathbf{F} \cdot (\mathbf{P_f^{(i)}} - \mathbf{P_p}) }{\Vert \mathbf{P_f^{(i)}} - \mathbf{P_p} \Vert }. \]
\(\mathbf{P_p}\) is the position vector of the mesh point and \(\mathbf{P_f}\) is the position vector of a face midpoint. \(\mathbf{F}\) is the upwind flux which is calculated as \[ \mathbf{F} = \sum_i w^{(i)} V_f^{(i)} \mathbf{n}_f^{(i)}. \]
\(\mathbf{F}\) is always calculated explicitely, even when the actual surface velocity is calculated implicitely.
The actual interpolation that is used for a simulation is calculated from both the linear and the upwind interpolation as \[ V_p = \beta V_{p, linear} + (1 - \beta) V_{p, upwind}. \]
\(\beta\) is the linearUpwindBlendingFactor.
In general it is desireable to choose \(\beta\) as large as possible to use a larger portion of the more accurate linear interpolation. However, choosing \(\beta\) too large makes the method unstable. From empirical tests we found that the method is stable if
\[ \frac{V_t \, \Delta t}{\Delta x (1 - \beta)} \lt 1 \]
is satisfied. \(\Delta t\) is the time step size, \(V_t\) is the tangential mesh velocity of the moving surface and \(\Delta x\) is the size of a mesh cell on the surface.
In general it should be noted that the interpolation does never guarantee conservation (conservation of mass in case of free surface flow and also conservation of energy in case of phase change).
Treatment of boundaries
For all points that are both on the targeted patch and also on one or more neighouring patches, the point normals are guaranteed to be orthogonal to these patches. This guarantees no displacement in the normal direction of neighbouring patches.
Laplace Smoothing
When enableing laplaceSmoothing, the boundary condition will attempt to re-distribute the mesh points on its surface to be equally spaced. This is done by moving every mesh point on the surface towards the midpoint of all its neighbours (see Laplacian smoothing for reference). Any surface-normal component of this correction is excluded to not artificially enlarge or shrink the mesh. The laplace correction is always calculated explicitely, even when the actual surface velocity is calculated implicitely.